레코드, 키의 정의 및 검색 트리

 트리에대한 알고리즘 공부에 앞서 트리에 대해 알아보는 시간을 가진다. 
대부분의 자료는 gmlwjd9405.github.io/2018/08/12/data-structure-tree.html 를 참조하였다. 알고리즘및 자료구조에관한 정리를 매우 잘 해놓은 블로그이니 참조하면 좋다.

레코드, 키의 정의 및 검색 트리

• 레코드
  • 개체에대해 수집된 모든 정보를 포함하고있는 저장단위
• 필드
  • 레코드에서 각각의 정보를 나타내는 부분
• 검색키
  • 다른 레코드와 중복되지 않는 각 레코드를 대표하는 필드
  • 키는 하나의 필드로 이루어질 수 도 있고 두개 이상의 필드로 이루어질 수 도 있다. 
• 검색트리
  • 각 노드가 규칙에 맞도록 하나씩의 키를 가지고있다. 
  • 이 키를 이용해 해당 레코드가 자정된 위치를 알 수 있다.  

TREE 자료구조의 특징

• TREE는 노드로 이루어진 자료구조이다.
  • 트리는 하나의 루트 노드를 가진다.
  • 루트노드는 0개 이상의 자식 노드를 가진다. 
  • 그 자식노드도 0개이상의 자식 노드를 가진다. 
• 트리는 노드(node)와 그 노드들을 연결하는 간선(edge)으로 이루어져있다. 
  
  • 트리의 노드 사이에는 CYCLE(순환)이 없다. 
  • 노드 사이엔 특정 순서가 있을수도 있고 없을수도있다. 
  • 각 노드는 부모도드로 연결이 있을수도있고 없을수도있다. 
  • 각 노드는 어떤 자료형으로도 표현이 가능하다. 
• 비 선형 자료구조이고계층적 관계를 표현한다.
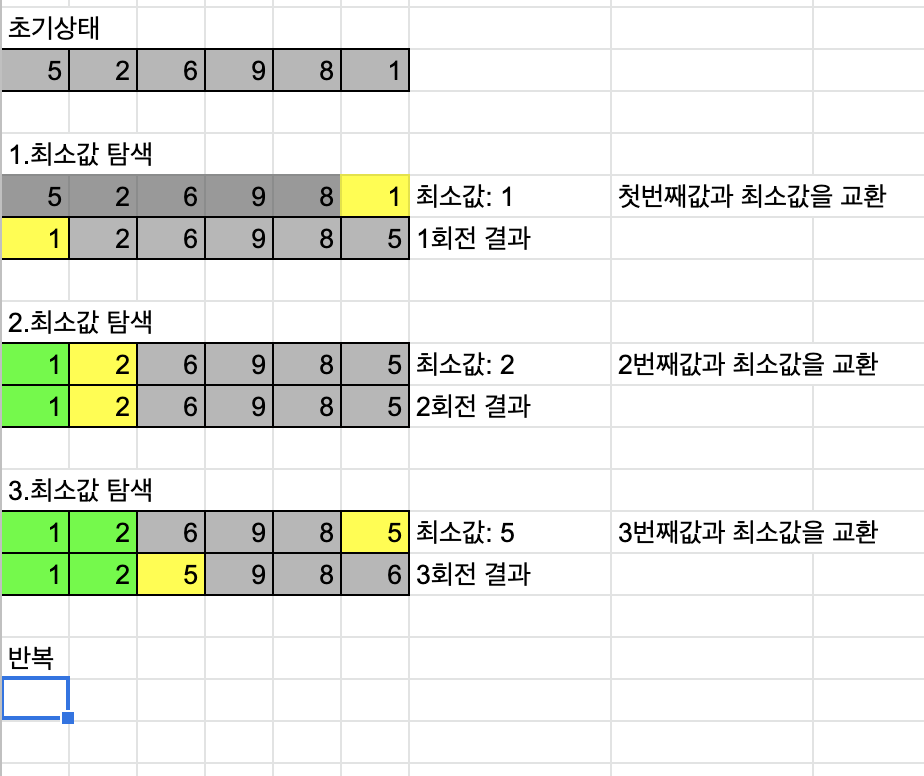
  • 주어진 배열에서 최솟값을 찾는다.
  • 그 값을 맨앞의 값과 교체한다.
  • 맨처음 위치를 뺀 나머지 리스트를 같은 방법으로 교채한다.
  • 하나의 원소만 남을때까지 위의 과정을 반복한다.
• 그래프의 한 종류이다. 
  • 사이클이 없는 연결그래프이다. 
  • DAG(Directed Acyclic Graph, 방향성이 있는 비순환그래프)의 한종류이다. 

TREE 와 연관된 용어

• 루트(root)노드: 부모가 없는 노드. 트리는ㄴ 하나의 루트노드만 가진다. 
• 단말(leaf)노드: 자식이 없는 노드.
• 내부(internal)노드: 루트도, 단말도 아닌 노드(부모와 자식이 있는 노드)
• 간선(edge): 노드들을 연결하는선. link, branch라고도 부른다. 
• 형제(sibling)노드: 같은 부모를 가지는 노드 
• 노드의 크기: 자신을 포함한 모든 자손 노드의 수
• 노드의 깊이(depth): 루트에서 특정 노드에 도달하기위해 거쳐야하는 간선의수
• 노드의 레벨(level): 루트에서 어떤 노드에 도달하기 위해 거처야하는 간선의 수 
• 노드의 차수(degree): 하위 트리의 개수 / 간선 수 degree = 각 노느가 가진 가지의 수
• 트리의 타수(degree of tree): 트리의 최대 차수
• 트리의 높이(height): 루트에서 부터 가장 깊숙히 있는 노드의 깊이.

TREE 의 종류

• 이진트리(Binary Tree)
  • 각노드가 최대 두개의 자식을 가질 수 있다.
  • 모든 트리가 이진트리는 아니다. 
  • 중위(in-order), 전위(pre-order), 후위(post-order)순회가 가능
• 이진 탐색트리
  • 모든 노드가 특정 순서를 따르는 속성이 있는 트리
  • 모든 외쪽 자식들 < 부모 < 오른쪽자식들의 순서를 가지고있는다.

이외의 균형/비균형, 전이진/완전이진/포화이진 트리 및  힙 트라이 같은 파생형은 출처에서 공부하면좋다. 

gmlwjd9405.github.io/2018/08/12/data-structure-tree.html

알고리즘을 공부하기위해 특징을 리마인드하기위한 포스팅이라서 구현방법같은 자료구조 영역은 생략한다. 자세한 사항은 출처를 확인하면 좋다. 

삽입정렬Insertion Sort

삽입정렬Insertion Sort알고리즘의 특징

**gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html 많은부분 참고했습니다.

• 손안의 카드를정렬하는 방법과 유사.

• 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 부분과 비교하여 자신의 위치를 찾아서 삽입한다. 

• 매순서마다 원소를 삽입할 수 있는 위치를 찾아서 해당 위치에 넣는다. 

  • 두번째 자료(index = 1 )부터 시작한다

  • 1번째 값이 0번째값보다 작으면 1번째 값을 0번째에 넣고 0번째 값을 1번째 자리에 넣는다.

  • 여기까지하면 인덱스 0,1이 정렬된 자료가된다. 

  • 2번째 값을 0,1번째 값과 비교한후 적절한 자리에 넣고 해당 자리의원소들은 뒤로 한칸씩 밀린다. 

  • 여기까지하면 인덱스 0,1,2가 정렬된 자료가 된다. 

  • 3번째 값을 정렬된 자료와 비교하여 적절한 자리에 넣고 원래 자리에있던 원소들은 한칸씩 뒤로간다. 

  • 여기까지하면 0,1,2,3이 정렬된 자료가된다. 

  • n까지 반복하면 0부터 n까지 정렬이 완료된다.

• 장점

  • 안정한 정렬방법이다.
  • 자료의 수가 적을경우 알고리즘이 매우 간단하다. 
  • 대부분 정렬이 된 상태일경우 효율적이다. 

• 단점

  • 자료의 이동이 많다. 
  • 자료가 많은 경우 적절하지못하다. 

알고리즘 예제

31      25     12    22     11 처음 상태.
31     [25]    12    22    11 두 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<25> 31    [12]    22    11 세 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<12> 25    31    [22]    11 네 번째 원소를 부분 리스트에서 적절한 위치에 삽입한다.
12    <22>  25    31    [11] 마지막 원소를 부분 리스트에서 적절한 위치에 삽입한다.
<11>    12    22    25    31 종료.}

삽입정렬Insertion Sort 코틀린 코드

fun insertionSort(arr: IntArray) : IntArray{
    var j = 0
    var key = 0


    for (i in 1 until arr.size) { //0번째 자료는 정렬된것으로 간주한다.
        key = arr[i]

        j = i
        while (--j >= 0 && key < arr[j]) {
            arr[j+1] = arr[j]
            arr[j] = key
        }


    }

    return arr
}

• 시간복잡도
  • 최선의경우
    • 비교횟수
      • 이동이 없이 1번의 비교만 이루어진다.
    • O(n)
  • 최악의 경우
    • 비교횟수
      • 모든 자료를 비교해야하기때문에 n개의 자료를 정렬할경우 n, n-1, n-2 ... 1 번의 비교를해야한다.
      • 비교는 O(n^2)번이라고할 수 있다.  
    • 교환횟수
      • 매번 교환이 이루어지기때문에 n, n-1, n-2 ... 1번의 교환이이루어진다. 
      • 교환이 O(n^2)번 이루어진다고할 수 있다.
    • 시간복잡도
      • O(n^2)

버블 정렬Bubble Sort

버블 정렬Bubble Sort 알고리즘의 특징

• 인접한 두 원소를 검사하여 정렬하는방법

• 느리지만 코드가 간단하여 자주 사용된다.(라고는 하는데 개인적으로 학부때 수업들을때말고는 사용해본적이 없긴하다.)

• 프로세스 방법

  • 인덱스 0 과 인덱스 1의 값을 비교한다.

  • 0번째의 값이 1번째의 값보다 크다면 스왑 한다.

  • 인덱스1과 인덱스 2의 값을 비교한다.

  • 1번째의 값이 2번째의 값보다 크다면 스왑 한다.

  • 인덱스를 증가시키면서 n 까지 반복한다.

  • n까지 반복하면 가장 큰 값이 맨 n에 위치하게된다.

  • 이제 인덱스 0부터 n-1 까지 반복한다.

  • 하나의 원소만 남을때까지 위의 과정을 반복한다.

• 장점

  • 구현이 단순하다. 

• 단점

  • 속도가 느리다.

알고리즘 예제

매우 적절할 버블정렬을 춤으로 나타낸 동영상이다.

youtu.be/lyZQPjUT5B4

버블 정렬Bubble Sort 코틀린 코드

fun bubbleSort(arr: IntArray): IntArray{
   var temp = 0
   for(i in arr.indices){
       for(j in 1 until arr.size - i)
           if(arr[j] < arr[j-1]) {
               temp = arr[j]
               arr[j] = arr[j - 1]
               arr[j - 1] = temp
           }
       }
    return arr
}

• 시간복잡도
  • O(n^2)
  • 정렬할 자료의 길이만큼 이중 반복을한다.

선택 정렬Selection Sort

선택 정렬Selection Sort 알고리즘의 특징

• 제자리 정렬(in-place sorting)의 하나이다.
  • 입력벼열(정렬되지 않은 값들) 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법.
• 해당 순서에 원소를 넣을 위치는 이미 정해져있고, 어떤 원소를 넣을지 선택하는 알고리즘.
  • 첫번째 순서에 첫번째 위치에 가장 최소값을 넣는다.
  • 두번째 위치엔 남은값중 최솟값을 넣는다.
  • n 번째 위치엔 남은 값중 최솟값을 넣는다.
• 프로세스 방법
  • 주어진 배열에서 최솟값을 찾는다.
  • 그 값을 맨앞의 값과 교체한다.
  • 맨처음 위치를 뺀 나머지 리스트를 같은 방법으로 교채한다.
  • 하나의 원소만 남을때까지 위의 과정을 반복한다.
• 장점
  • 자료의 이동 횟수가 미리 결정된다.
• 단점
  • 안정성을 만족하지않는다.

알고리즘 예제

선택정렬의 코틀린 코드

fun main(){

    print(selectionSort(intArrayOf(3,6,1,7,5,4,9)).joinToString(","))
    //1,3,4,5,6,7,9
}

fun selectionSort(arr: IntArray): IntArray{
   var minIdx = 0
   var temp = 0
   for(i in arr.indices){
       minIdx = i
       for(j in i+1 until arr.size   ){
          if(arr[minIdx] > arr[j]) {
              minIdx = j
          }
       }

       if(minIdx != i){
           temp = arr[i]
           arr[i] = arr[minIdx]
           arr[minIdx] = temp
       }

   }

    return arr
}

• 시간복잡도
  • O(n^2)
  • 정렬할 자료의 길이만큼 이중 반복을한다.

앞으로 공부할 알고리즘. 공부가 끝나면 블로그에 정리 후 링크를 달아두기로한다. 

1. 정렬
  1.기본적인 정렬 알고리즘
    1. 선택 정렬Selection Sort
    2. 버블 정렬Bubble Sort
    3 .삽입 정렬Insertion Sort
  2. 고급 정렬 알고리즘
    1. 병합 정렬Merge Sort
    2. 퀵 정렬Quick Sort
    3. 힙 정렬Heap Sort
  3. 비교 정렬 시간의 하한
  4. 특수 정렬 알고리즘
    1. 기수 정렬Radix Sort
    2. 계수 정렬Counting Sort

2.선택 알고리즘
  1 평균 선형 시간 선택 알고리즘
  2 최악의 경우에도 선형 시간을 보장하는 선택 알고리즘

3.검색 트리  
  1. 레코드, 키의 정의 및 검색 트리
  2. 이진 검색 트리 
    1. 이진 검색 트리에서 검색
    2. 이진 검색 트리에서 삽입
    3 .이진 검색 트리에서 삭제
  3, 레드 블랙 트리
    1. 레드 블랙 트리에서 삽입
    2. 레드 블랙 트리에서 삭제
    3. 레드 블랙 트리의 작업 성능 분석
  4. B-트리
    1. B-트리에서 검색
    2. B-트리에서 삽입
    3. B-트리에서 삭제
    4. B-트리의 작업 성능 분석
  5. 다차원 검색 트리
    1. KD-트리
    2. KDB-트리
    3. R-트리
    4. 그리드 파일

4. 해시 테이블
  1. 해시 테이블 : 검색 효율의 극단
  2. 해시 함수
    1. 나누기 방법
    2. 곱하기 방법
  3. 충돌 해결
    1. 체이닝
    2. 개방 주소 방법
  4. 해시 테이블에서 검색 시간 분석

5. 집합의 처리
  1. 연결 리스트를 이용한 집합의 처리
    1. 작업의 개요
    2. 수행 시간
  2. 트리를 이용한 집합의 처리
    1. 기본 원리
    2. 연산의 효율을 높이는 방법

6. 동적 프로그래밍
  1. 어떤 문제를 동적 프로그래밍으로 푸는가
  2. 행렬 경로 문제
  3. 돌 놓기 문제
  4. 행렬 곱셈 순서 문제
  5. 최장 공통 부분 순서LCS

7. 그래프
  1. 그래프
  2. 그래프의 표현
    1. 인접 행렬을 이용한 방법
    2. 인접 리스트를 이용한 방법
    3 .인접 배열과 인접 해시 테이블
  3. 너비 우선 탐색BFS과 깊이 우선 탐색DFS
  4. 최소 신장 트리
    1. 프림 알고리즘
    2. 크루스칼 알고리즘
    3 .안전성 정리
  5. 위상 정렬Topological Sorting
  6. 최단 경로
    1. 다익스트라 알고리즘(음의 가중치를 허용하지 않는 경우 )
    2. 벨만-포드 알고리즘(음의 가중치를 허용하는 경우)
    3 .모든 쌍 최단 경로 알고리즘
    4 .사이클이 없는 그래프의 최단 경로
  7. 강연결 요소

8. 그리디 알고리즘
  1. 전형적인 그리디 알고리즘의 구조
  2. 그리디 알고리즘으로 최적해가 보장되지 않는 예
    1. 이진 트리의 최적합 경로 찾기
    2. 보따리 문제
    3 .동전 바꾸기
  3. 그리디 알고리즘으로 최적해가 보장되는 예
    1. 최소 신장 트리
    2. 회의실 배정 문제
    3 .그 밖의 예
  4. 매트로이드 : 그리디 알고리즘으로 최적해가 보장되는 공간 구조
    1. 매트로이드의 정의와 예
    2. 매트로이드의 확장과 포화
    3. 매트로이드 구조이면 그리디 알고리즘으로 최적해 보장
    ★ 4. 문제 공간 탐색 관점에서 본 매트로이드

9. 문자열 매칭
  1. 원시적인 매칭 방법
  2. 오토마타를 이용한 매칭
  3. 라빈-카프 알고리즘
  ★ 4. KMP 알고리즘
  5. 보이어-무어 알고리즘

10. NP-완비
  1. 문제의 종류
  2. Yes/No 문제와 최적화 문제
  3. NP
  4.. 다항식 시간 변환
  5. NP-완비
  6. NP-완비 문제들
  7. NP-하드를 최적화 문제로 확장하기
  ★ 8. 근사해 구하기
  ★ 9. 현상금 걸린 문제들

11.상태 공간 트리의 탐색
  1. 상태 공간 트리
  2. 백트래킹
    1. 미로 찾기 문제
    2. 색칠 문제
  3. 한정 분기
  4. A* 알고리즘
    1. 최단 경로 찾기 문제
    2. TSP
  Drift 공간 탐색과 끌개